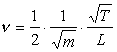
n
[Hz]
(frequenza)
T [N] (tensione)
m [kg/m] (massa lineare)
L [m] (lunghezza della parte vibrante)
Manuale di Acustica
Dedicato a Brian May, chitarrista dei Queen
Alberto Orlandini
| Indice | |
| Il suono | Il suono |
| Velocit� | Velocit� |
| Velocit� nell'aria in funzione della temperatura | |
| Frequenza | Frequenza |
| Frequenza di suoni generati da una corda | |
| Note musicali | Note musicali |
| La scala naturale | |
| La scala temperata | |
| Tabella delle frequenze delle note musicali | |
| Lunghezza d'onda | Lunghezza d'onda |
| Effetto Doppler | Effetto Doppler per le onde sonore |
| Effetto Doppler per la luce | |
| Intensit� | Intensit� |
| Pressione sonora | |
| Potenza sonora | |
| Livelli e decibel | Livelli e decibel |
| Livello di pressione sonora | |
| Livello di potenza sonora | |
| Bibliografia | Bibliografia |
Un�onda sonora consiste in lievi variazioni della pressione atmosferica che seguono una legge armonica. In termini matematici:
| p = patm + ps , dove ps = p0�sin(2p n t) |
p [Pa]
(pressione) |
| ps � la pressione sonora o pressione relativa, e varia nel tempo. | |
| patm � la pressione atmosferica quando c�� silenzio, ed � un valore costante e molto pi� grande di ps. |
|
Il suono non si propaga nel vuoto perch� non c�� pressione.
Velocit� [m/s]
La velocit� rappresenta la
distanza percorsa dall�onda sonora in un secondo.
La velocit� del suono dipende dal mezzo di propagazione e dalla temperatura.
Pare che Isaac Newton sia stato il primo ad aver misurato la velocit� del suono
nell'aria.
velocit� nell�aria a 20�C
= 343 m/s
velocit� nell�acqua a 20 �C = 1525 m/s
velocit� nel ferro = 5000 m/s
Velocit� nell�aria in funzione della temperatura
La velocit� del suono nell�aria dipende dalla temperatura e pu� essere ottenuta con la formula seguente:
| v = 0,6 T + 331 | v [m/s] (velocit� del
suono nell�aria) T [�C] (temperatura in gradi centigradi) |
Frequenza [Hz = s-1]
La frequenza rappresenta il numero di oscillazioni che l�onda compie in
un secondo.
Un orecchio umano medio riesce a percepire suoni con frequenza compresa
tra 40 Hz e 15000 Hz.
Per quanto riguarda l�emissione, se si considera solo la frequenza principale � quella propria della nota emessa � escludendo tutte le altre armoniche,
il
rango vocale umano va da 70 Hz a 1000 Hz o pi�, cio� da un Re(1) a un Do(5) o
pi�.
In realt�
pochi esseri umani riescono realmente a coprire un rango cos� ampio � si tratterebbe quasi di 4 ottave!
In base alla frequenza i suoni vengono classificati in note musicali.
Frequenza di suoni generati da una corda
La formula seguente fu
ipotizzata da Galileo Galilei e poi risult� essere corretta.
Essa restituisce la frequenza di un suono generato da una corda
vibrante:
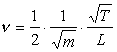 |
n
[Hz]
(frequenza) |
La vibrazione della corda produce anche altri suoni le cui frequenze sono multiple di quella restituita dalla formula. Tali suoni sono detti armoniche.
Gli esseri umani distinguono i suoni in base alla frequenza, o meglio in base al rapporto tra le frequenze. L�orecchio umano ha una percezione logaritmica della frequenza: pi� precisamente, ad ogni ottava corrisponde un raddoppiamento o un dimezzamento di frequenza.
Il problema di costruire
una scala musicale consiste nello scegliere una successione di toni, chiamati
note, con intervalli opportuni, in modo da permettere un dato tipo di musica.
In particolare � molto importante sapere che cosa avviene quando due o pi�
note sono suonate insieme (armonia funzionale).
Fin dai tempi di Pitagora � noto che due suoni provocano una sensazione piacevole solo se il rapporto tra le loro due frequenze � quello di due numeri interi piccoli (1/2, 2/3, 3/4...). In tal caso i suoni sono consonanti. Altrimenti si dicono dissonanti.
Nella tabella seguente sono riportati i rapporti di consonanza pi� comuni in musica.
| ottava | 2:1 |
| quinta | 3:2 |
| quarta | 4:3 |
| terza maggiore | 5:4 |
| terza minore | 6:5 |
| sesta maggiore | 5:3 |
La scala naturale viene attribuita al filosofo greco Aristoxenus Tarentinus (500-400 a.C.) e consiste di una successione di note con frequenze crescenti.
Una volta fissata la frequenza della prima nota - il do della scala -, le frequenze delle altre sono determinate dai rapporti indicati nella tabella seguente. Con l'ultimo Do comincia l'ottava successiva e l'operazione pu� ripetersi.
| Do | 1 |
| Re | 9/8 |
| Mi | 5/4 |
| Fa | 4/3 |
| Sol | 3/2 |
| La | 5/3 |
| Si | 15/8 |
| Do | 2 |
Il rapporto � riferito alla frequenza della prima nota della scala.
Notiamo che nella scala naturale i rapporti fra le frequenze di due note che differiscono tra loro di un tono non sono sempre gli stessi. Di conseguenza una data melodia non pu� essere suonata a partire da una nota arbitraria della scala. Per esempio, una melodia che inizia con le due note Do e Re (rapporto 9/8) non pu� essere trasposta un tono pi� alta, poich� il rapporto fra le frequenze del Mi e del Re � molto vicino ((5/4)/(9/8) = 10/9), ma non identico a 9/8.
Per
ovviare a questo inconveniente, si fa uso della cosiddetta scala
temperata, che
costituisce il compromesso adottato nella musica occidentale.
Essa si ottiene dividendo un intervallo di ottava in dodici intervalli, detti semitoni, tali che il rapporto delle frequenze di due note
successive sia costante e pari a ![]() =
1,059463
=
1,059463
La tabella seguente permette un confronto tra la scala naturale e la scala temperata:
|
Nota |
Scala temperata | Scala naturale | |||
| Esponente | Potenza | Valore | Frazione | Valore | |
| Do | 0 | 20/12 | 1,000 | 1/1 | 1,000 |
| Do# / Reb | 1 | 21/12 | 1,059 | ||
| Re | 2 | 22/12 | 1,122 | 9/8 | 1,125 |
| Re # / Mib | 3 | 23/12 | 1,189 | ||
| Mi | 4 | 24/12 | 1,260 | 5/4 | 1,250 |
| Fa | 5 | 25/12 | 1,335 | 4/3 | 1,333 |
| Fa# / Solb | 6 | 26/12 | 1,414 | ||
| Sol | 7 | 27/12 | 1,498 | 3/2 | 1,500 |
| Sol# / Lab | 8 | 28/12 | 1,587 | ||
| La | 9 | 29/12 | 1,682 | 5/3 | 1,666 |
| La# / Sib | 10 | 210/12 | 1,782 | ||
| Si | 11 | 211/12 | 1,888 | 15/8 | 1,875 |
| Do | 12 | 212/12 | 2,000 | 2/1 | 2,000 |
Se
si guardano i valori delle potenze di ![]() e
i valori delle frazioni, � sorprendente quanto essi siano simili. Per la musica
� una fortuna che la differenza tra le due scale sia impercettibile.
e
i valori delle frazioni, � sorprendente quanto essi siano simili. Per la musica
� una fortuna che la differenza tra le due scale sia impercettibile.
Quale delle due scale � la pi� giusta?
L�orecchio umano percepisce le frazioni o gli esponenti di ![]() ?
?
Una risposta certa non esiste, ma poich� l�orecchio umano non riesce a
percepire alcuna differenza tra le due scale, non � essenziale trovare una
risposta.
Il
rapporto ![]() =
1,059463 � lo stesso valore che si troverebbe se si calcolasse il rapporto tra
le ampiezze di due tasti consecutivi di una chitarra. Il dodicesimo tasto divide
la corda esattamente a met�. Per maggiori informazioni vedere la sezione Programmi
=
1,059463 � lo stesso valore che si troverebbe se si calcolasse il rapporto tra
le ampiezze di due tasti consecutivi di una chitarra. Il dodicesimo tasto divide
la corda esattamente a met�. Per maggiori informazioni vedere la sezione Programmi
Tabella delle frequenze delle note musicali
Per convenzione la nota di
riferimento � il La centrale
Sappiamo dai flauti che nel Rinascimento esso era pi� alto di 460 Hz.
Nel 1859 il La francese fu ufficialmente fissato a 435 Hz. In seguito tale
frequenza fu adottata come altezza internazionale nel 1887 a Vienna. Tuttavia il
La britannico era ancora fissato a 440 Hz.
Oggi il La � convenzionalmente fissato a 440 Hz ovunque.
Ci sono modi differenti per indicare le ottave. Di solito 440 Hz � la frequenza del La(3), ma a volte � possibile trovare che 440 Hz � il La(4) o il La(2). Qui sotto si assume che 440 Hz sia la frequenza del La(3).
|
|
|
|
Il La basso delle chitarre (5� corda) � 110 Hz
Lunghezza d�onda [m]
La lunghezza d�onda � la
distanza tra due punti consecutivi in cui la pressione atmosferica � minima o
massima.
Conoscendo velocit� e
frequenza, � possibile ricavare la lunghezza d�onda con la formula seguente:
| l = c / n | l
[m] (lunghezza d�onda) |
La lunghezza d�onda dei suoni udibili va dai centimetri ai metri.
Effetto Doppler per le onde sonore
Se la sorgente o il ricevente di un onda sono in movimento, le velocit� non si sommano con la velocit� propria dell�onda nel mezzo. La velocit� di propagazione dell�onda nel mezzo infatti non varia. Ci� che varia � la frequenza.
Le formule seguenti conterranno i seguenti simboli:
| l | [m] | lunghezza d�onda |
| n | [Hz] | frequenza |
| c | [m/s] | velocit� propria del suono nel mezzo |
| v | [m/s] | velocit� della sorgente o del ricevente rispetto al mezzo positiva se provoca avvicinamento tra sorgente e ricevente negativa se provoca allontanamento tra sorgente e ricevente |
Sorgente in movimento rispetto al mezzo:
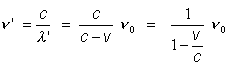 |
Ricevente in movimento rispetto al mezzo:
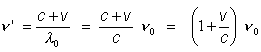 |
Quando sia la sorgente sia il ricevente si muovono rispetto al mezzo:
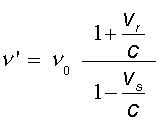 |
vr =
velocit� del ricevente rispetto al mezzo vs = velocit� della sorgente rispetto al mezzo positive se provocano avvicinamento
tra sorgente e ricevente |
Se anche il mezzo � in
movimento (ad esempio, c�� vento), vr e vs devono
comunque essere espresse rispetto al mezzo. Tuttavia in tal caso pu� risultare
pi� comodo continuare a esprimere vr e vs in un sistema
di riferimento solidale con la terra, sostituendo la velocit� dell�onda c con:
c� = c + vm (dove vm � la velocit� del mezzo rispetto
alla terra).
Inoltre se il moto della sorgente o del ricevente non avvengono lungo la direzione di propagazione del suono, ma in una direzione inclinata di un angolo a, il rapporto v/c deve essere moltiplicato per cos(a)
La differenza tra le
variazioni di frequenza nei due casi (sorgente in movimento, ricevente in
movimento) � una differenza reale che si riscontra sperimentalmente.
Tale differenza ha per�
anche una notevole importanza teorica, perch� mostra che le due
situazioni sono realmente diverse.
| Effetto Doppler per le onde sonore |
| Non conta
il moto relativo tra sorgente e ricevente, ma contano i moti assoluti di entrambi rispetto al mezzo |
Effetto Doppler per la luce e le onde elettromagnetiche
Per le onde elettromagnetiche e per la luce, che si propagano anche nel vuoto, il mezzo non conta pi�. Conta invece solo il moto relativo tra sorgente e ricevente.
Con le opportune correzioni relativistiche di Lorentz si ottiene che
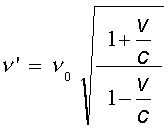 |
v = velocit�
relativa tra sorgente e ricevente
positiva se si
avvicinano |
Per valori piccoli di v/c , tale espressione pu� essere approssimata a una delle due espressioni che avevamo trovato per le onde sonore.
Infatti per x tendente a
zero 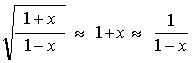
Se una sorgente si muove
con velocit� maggiore della velocit� delle onde
- per la luce non �
possibile
- per il suono, non ci
saranno onde davanti alla sorgente;
in tal caso le onde si accumulano dietro la sorgente formando
un onda d�urto
che viene udita come un boom sonico (aerei supersonici)
L�intensit� sonora � comunemente chiamata volume.
Pressione sonora [Pa = N/m2]
La pressione sonora rappresenta la forza esercitata dall�onda sonora su un m2 di superficie.
Il timpano � sempre soggetto alla pressione atmosferica, che � pressoch� costante. In presenza di un suono o di rumore, il timpano � anche soggetto alla pressione esercitata dall�onda sonora, che si somma alla pressione atmosferica. Si ricorda che, indicando con ps la pressione sonora, la pressione totale esercitata sul timpano � data da:
p = patm + ps , dove ps = p0�sin(2p n t)
Il volume percepito �
tanto pi� alto quanto pi� alta � la differenza di pressione
tra i punti in cui la pressione � massima e i punti in cui � minima.
La pressione sonora � una
grandezza relativa all�ascoltatore
ed � inversamente proporzionale alla distanza dalla sorgente.
Potenza sonora [W]
La potenza sonora rappresenta l�energia acustica emessa da una sorgente in un secondo.
La potenza istantanea
ha generalmente un valore molto inferiore alla potenza massima
(Ad esempio: uno speaker
che sull� etichetta di fabbricazione riporta una potenza
nominale massima di 50 W, non raggiunger� mai quella potenza. Con un
normale ascolto la potenza istantanea rimarr� sempre 1 W circa)
La potenza sonora � una grandezza relativa unicamente alla sorgente.
Livelli [dB]
Si definisce livello il
logaritmo del rapporto tra una data quantit� e una quantit� di
riferimento della stessa specie.
L�unit� di misura dei
livelli sonori � il decibel, simbolo dB.
Lo strumento di misura �
il fonometro.
E� una grandezza relativa all�ascoltatore, e dipende dalla distanza dalla sorgente.
Lp = 10 Log10 [ ( p / p0 )2 ] = 20 Log10 [ ( p / p0 ) ]
p0 � la pressione sonora di riferimento, che per convenzione vale 20 �10-6 Pa
E� una grandezza relativa unicamente alla sorgente, e non dipende dalla distanza.
Lw = 10 Log10 ( W / W0 ) = 10 Log10 W + 120 dB
dove W � la potenza
istantanea della sorgente espressa in watt
[W]
W0 � la potenza
sonora di riferimento, che per convenzione vale 10-12 W
Livello di pressione sonora in funzione della distanza dalla sorgente
La pressione sonora � inversamente proporzionale alla distanza dalla sorgente
LB � LA = � 20 Log10 ( rB / rA )
DL
= � 6 dB
ogni volta che si raddoppia la distanza dalla sorgente
DL
= � 20 dB
ogni volta che si aumenta la distanza dalla sorgente di un fattore 10.
Livello di pressione
sonora in funzione della distanza dalla sorgente
quando � noto il
livello di potenza sonora
Lp = Lw � 20 Log10 ( r ) � 10
dove r � la distanza dalla sorgente espressa in metri
Alcune formule sono prese da
libri, conoscenza comune e altre fonti.
Molte parti, soprattutto le parti relative alle note musicali e l'acustica, � stata
scritta dallo stesso Alberto Orlandini.
L'esposizione degli argomenti, cos� come l'organizzazione dell'esposizione, � stata curata da Alberto
Orlandini.